这是一份最科学的抛硬币教程。
我们常会反复纠结某个问题而难以迅速作出决定,比如,今晚吃炸酱面还是麦当劳;又比如,要不要接受某个工作机会;或者是今晚要不要去跟 TA 表白

这时,很多人会抛个硬币,用硬币的正反面替自己做出选择。甚至在一些重大场合,人们也常用抛硬币来做重要决定,比如世界杯球赛中,裁判员会通过抛硬币决定哪只队伍先开球。

初中数学课本告诉我们,抛一枚质地均匀的硬币,得到正反面的概率相等。因此,人们认为硬币替自己做出的选择一定是公正的,没有私心的。不少数学家也做过实验证明,当抛硬币次数足够多时,得到正反面的频次接近 1:1,包括曾抛了 2 万多次硬币的数理统计学创始者卡尔皮尔逊(Karl Pearson)。
但如果我现在告诉你,抛硬币得到两面向上的概率其实不相等,你又怎么看?
两面概率不相等
最近,一群无聊的科学家聚在一起,用 46 种不同的硬币抛了 350757 次,总耗时约 20 个小时。然后他们发现,抛出的硬币落下后,向上的那一面和硬币抛出前的初始面相同的概率略高,约为 51%。

他们就这样抛了 20 个小时的硬币。来源:Coin Tossing Team via YouTube
也就是说,假如你将硬币抛离手中时,它是正面向上,那最终硬币落下时,其正面向上的概率更高,反之亦然。
他们还发现,一些人抛硬币得到和起始面相同的那一面的概率更高;而另一些人则更接近理论值,即得到两面的概率都是 50%。他们将这项研究发表了在预印本网站 arXiv 上,还未经同行评审。
很显然,这说明,特定的抛硬币方式,或许可以让特定面向上的概率更高。
那么,有没有可能通过练习,让抛出去的硬币落下时,永远是自己想要的那一面向上呢?
理论上是可以的。
数学家佩尔西戴康尼斯(Persi Diaconis)在成为美国斯坦福大学的数学和统计学教授之前,曾做过魔术师。他经常研究与赌博相关的数学,比如如何洗牌、如何掷骰子,当然也包括如何抛硬币。

热衷于纸牌、骰子、轮盘等的斯坦福数学家佩尔西?戴康尼斯。图片来源:Stanford University
早在 2007 年,戴康尼斯和他的团队就在论文中展示了一个抛硬币装置,这个装置将硬币抛出后落到指定位置,最终硬币向上的那一面在 100%的情况下都与它的起始面相同。

戴康尼斯和同事做出的抛硬币装置,抛出的硬币能100%得到与起始面相同的那一面。Diaconis et al, 2007
而人类在用手抛硬币时,也可以达到这样的效果,比如一些魔术师就可以通过一些技巧控制抛硬币的结果。

魔术师能控制抛硬币的结果。来源:SCAM NATION via youtube
其实如果掌握了原理,多加练习,你也可以做到。所以我们就先来学习一下原理,然后大家回家自己练习。
首先我们需要知道,标准情况下,抛向空中的硬币是怎样运动的。
忽略空气阻力的影响,当我们将硬币抛向空中,硬币会沿着一个位于硬币平面且平行于地面的轴,做翻转运动。学过物理的朋友们可以很快反应过来,这个轴正好是硬币旋转的角动量(angular momentum)所在的直线。

来源:Numberphile via YouTube

来源:Numberphile via YouTube,制图:冬鸢
然后我们用一点简单的中学物理来分析一下硬币的运动。
假设硬币以初速度vz从距地面高度z0的手中被抛出,t 秒后落回到手上,那么通过z0+ tvz?(g/2)(t)2= z0可以计算出t = vz/(g/2)。
假设硬币在空中每秒翻转 次。在抛出硬币到硬币回到手上的过程中,如果硬币翻转了偶数次(即 2j vz/(g/2) 2j+1,其中 j 为整数),那么硬币最终向上的一面与初始面相同;如果翻转了奇数次(即 2j+1 vz/(g/2) 2j+2,其中 j 为整数),则与初始面相反。

来源:wikiHow via YouTube
所以只要你能精确控制硬币的初速度、高度和翻转速度,就能精确控制抛硬币的结果(虽然可能有点强人所难)。
如果我们在硬币翻转了整数次时,做出转速关于时间t的图像,可以得到很多条双曲线,如下图所示:
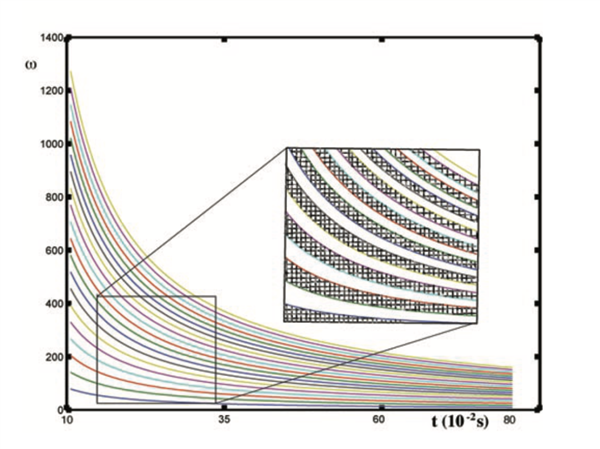
图片来源:Diaconis et al, 2007
假如硬币初始面为正面,而翻转速度和时间(,t)落在图中的阴影里,最终正面向上;若是转速和时间位于阴影之外的空白部分,结果则是反面朝上。
但是,此时阴影部分的面积和空白部分的面积是相等的,得到正面和反面的概率仍然是 1:1。如果要出现上文提到的偏差,又该如何操作呢?
运动
以上分析是基于标准情况,抛出的硬币沿着平行与地面的轴翻转,也就是硬币旋转的角动量矢量平行于地面。
但戴康尼斯指出,这只是一种特殊情况。实际上,很多人抛出的硬币在空中旋转时,角动量是与地面不平行的。

仔细观察可以发现这枚硬币在空中并不是绕着平行与地面的轴翻转的。来源:Sound/Video Impressions via youtube
我们可以用如下的模型来解释:
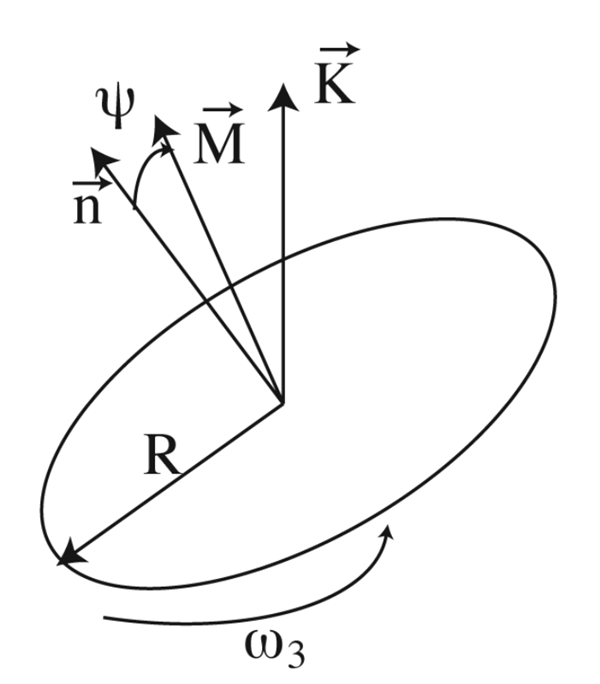
图片来源:Diaconis et al, 2007
假设硬币抛出时正面向上,则垂直于硬币平面的法线( n )与角动量(M)会存在一个夹角(),当硬币转动的轴与地面不平行(即 不为 90)时,硬币法线 n 就会绕着角动量 M 旋转,这也叫进动(precession)。

戴康尼斯正在解释硬币翻转中的进动。来源:Numberphile via YouTube
若硬币在抛出后的t时刻落回手上,当此时硬币法线N(t)与垂直地面方向的向量 K 的夹角余弦 (t) 大于 0 时,硬币正面向上;小于 0 时,反面向上(起始面为正面)而对于这个余弦 (t),我们可以用 (t)=cos2 +sin2 cos(Nt) 这个式子来计算,其中 N 为硬币法线绕角动量旋转的角速度。
如果我们将硬币的法线矢量N(t)在空中划过的区域看做一个球面,在这样的运动方式下,法线在上半球(正面向上)停留的时间是大于或等于在下半球(反面向上)停留的时间的。
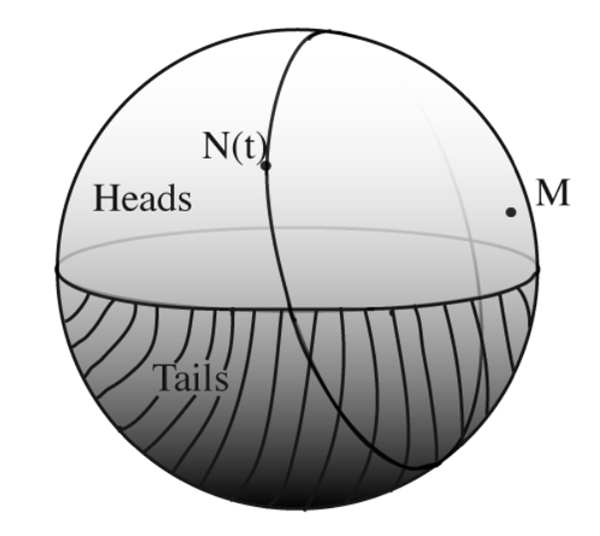
图片来源:Diaconis et al, 2007
最终可以算出,如果硬币的起始面为正面,那么硬币落回手上时正面向上的概率与 的关系是:
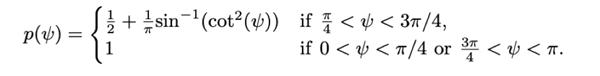
用图像表示就是
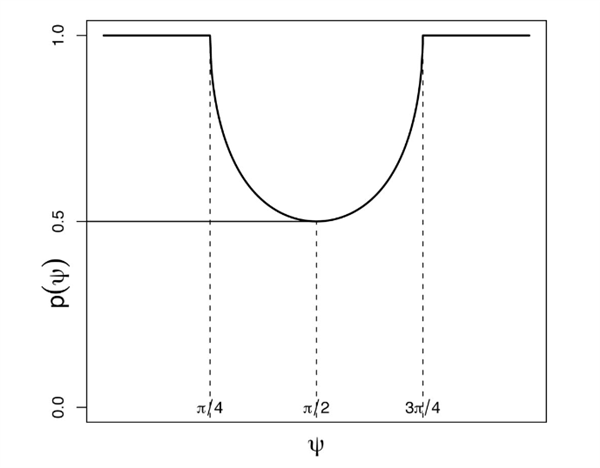
图片来源:Diaconis et al, 2007
由此可以直观地看到,在硬币初始面为正面时,只有当 为直角,硬币落下时正面朝上的概率才是 1/2,其余情况下都大于 1/2。
而当 小于 45时,硬币虽然也在旋转,但实际上整个过程中,并没有翻转到另一面。因此,在这种情况下,不论硬币抛得有多高,最终落下来时依然是和抛出时保持相同的一面向上这便是抛硬币魔术师所使用的手法。

魔术师抛出的硬币在空中没有翻转至另一面。来源:SCAM NATION via YouTube而当 为 0时,硬币甚至可以没有竖直方向的翻转,完全直上直下。

来源:Numberphile via YouTube
事实上,这种运动方式在我们生活中非常常见,比较典型的,就是我们的地球。地球在自转的同时,赤道平面的法线也在绕一个轴转动:

看这地球的旋转像不像正在翻转的硬币?来源:Steven Sanders via youtube
总结一下就是,因为很多人抛出的硬币在空中翻转时存在进动,导致在给定硬币初始面的情况下,会使得最终硬币落回手上时,正反面向上的概率不相等。
不过,由于大多数人抛硬币的时候,不会关注硬币的起始面。因此,在起始面随机的前提下,抛硬币的最终结果,正反面概率仍然是 1:1(预印本论文中有证明过程)。
所以,以后如果和别人抛硬币打赌,你可以练一练上面教的抛硬币技巧来作弊;如果是别人抛硬币,那就让他不要用手接,让硬币直接掉地上,因为这会使硬币再弹起来,到空中再翻转几圈,使结果更加随机。

硬币掉在地上之后再弹起来。来源:Numberphile via YouTube
参考文献
[1]https://statweb.stanford.edu/~cgates/PERSI/papers/dyn_coin_07.pdf
[2]https://arxiv.org/abs/2310.04153
[3]http://gauss.stat.su.se/gu/sg/2012VT/penny.pdf
[4]https://en.wikipedia.org/wiki/Precession
[5]https://en.wikipedia.org/wiki/Angular_momentum
[6]https://en.wikipedia.org/wiki/Persi_Diaconis
[7]https://www.youtube.com/watch?v=AYnJv68T3MM
[8]https://www.youtube.com/watch?v=A-L7KOjyDrE
[9]https://www.youtube.com/watch?v=qlVgEoZDjok
[10]https://www.youtube.com/channel/UCZF_uxG9yEiuUkaFol16IBg
策划制作
来源丨环球科学
作者|冬鸢
责编丨杨雅萍




















